
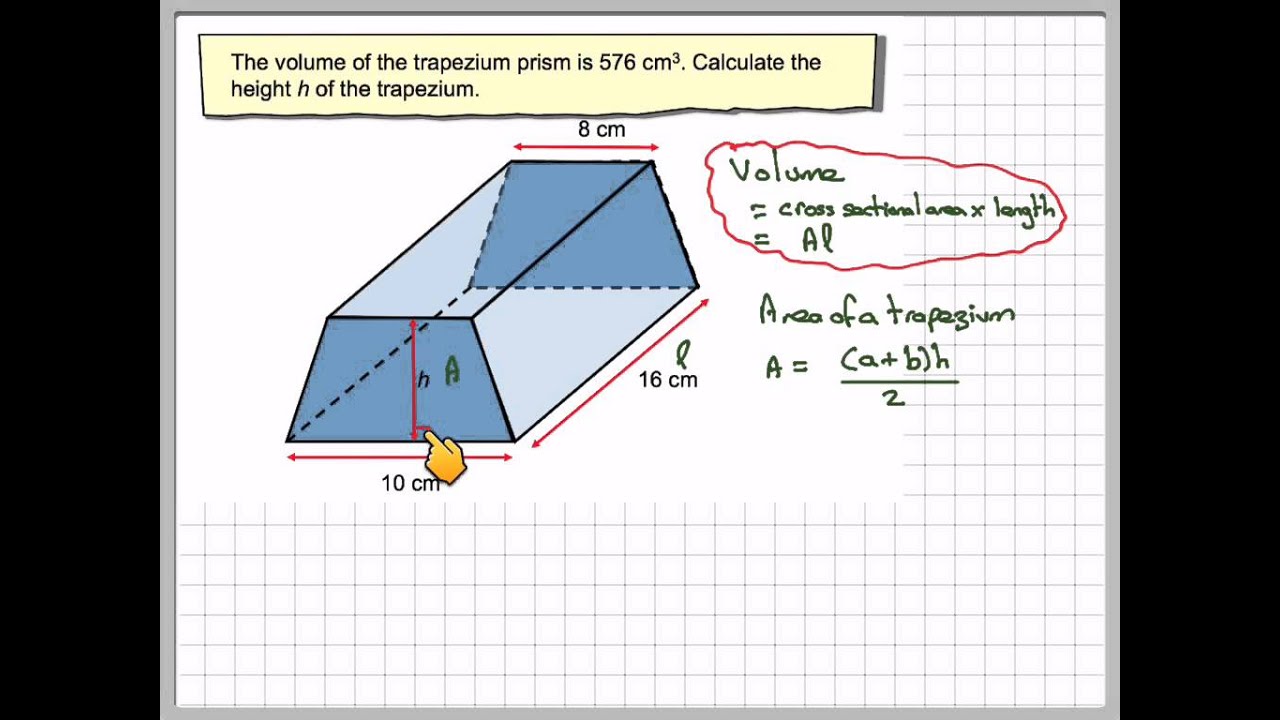
The perimeter of the base is the sum of the lengths of the sides. Solution: Using the Pythagoras theorem, the slant height or the non-parallel side = √(16+1) = √17 = 4.123 ft Step 5: Put the values in the formula, 2B + Lateral Surface Area(PH), to get the total surface area of the hexagonal prism.Įxample: Determine the total surface area of the trapezoidal prism.Find the base area B by putting the above values in the formula, (b1+b2)h/2 Step 4: Identify b1 and b2 (lengths of the bases) of the trapezoid and h (height) of the trapezoid.Step 3: Put the values in the formula, (a+b+c+d) × H or PH, to find the lateral surface area of the hexagonal prism.Step 2: Identify the length H of the prism.Add these 4 values in order to find the perimeter P. Step 1: Identify the four sides of the trapezium - a, b, c, and d, representing the widths of the four rectangles.Note that all measurements are of the same units. Here are the steps to calculate the surface area of a trapezoidal prism.
#Trapezoidal prism how to#
How to Calculate the Surface Area of a Trapezoidal Prism? Thus, the total surface area of a trapezoidal prism is h(b+d)+l(a+b+c+d) square units. TSA of the trapezoidal prism = h (b + d) + l (a + b + c + d). Therefore, the total surface area of the trapezoidal prism (TSA) = 2 × h (b + d)/2 + (a × l)+(b × l) + (c × l) + (d × l) = h (b + d) + Substituting the values from equation (2) and equation (3) in the TSA formula, which is represented by equation (1): The lateral surface area of the trapezoidal prism (LSA) is the sum of the areas of each rectangular surface around the base that means, LSA = (a × l) + (b × l) + (c × l) + (d × l) - (3) Thus, the area of trapezoidal base = h (b + d)/2 - (2) We already know that the total surface area of the trapezoidal prism (TSA) = 2 × area of base + lateral surface area - (1)Īlso, the area of a trapezoid = height(base1 × base 2)/2.
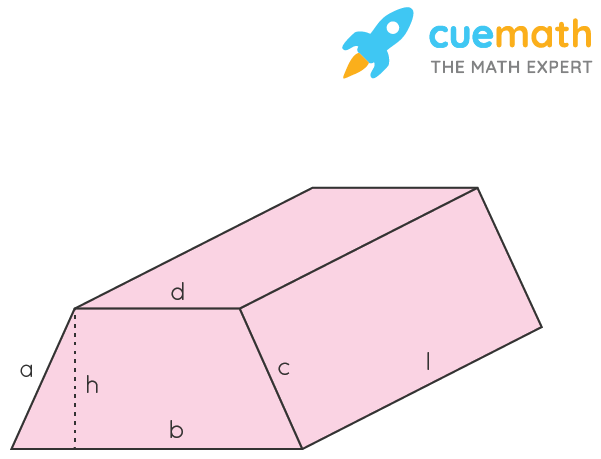
We know that the base of a prism is in the shape of a trapezoid. Derivation of Surface Area of Trapezoidal Prism


 0 kommentar(er)
0 kommentar(er)
